| The normal at [t]
passes through (X, Y)
if |
tX -Y/t
= c(t2- )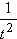
|
| i.e. if |
ct4-t3X
+
tY -c = 0 |
|
ct4-Xt3
+ Yt-c = 0 |
| The root of t1,
t2,
t3,
t4
of
this quartic equation are the 4 conormal points |
| and |
t1t2t3t4
= 
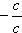= -1 |
| and |
y1y2y3y4
= (ct1)(ct2)(ct3)(ct4)
= c4t1t2t3t4
= - c4 |
| and |
X/c
= (t1
+
t2
+ t3
+
t4) 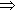 X
=
c(t1+
t2
+
t3
+ t4) |
|
Y/c
= -(t1t2
t3
+
t1t2t4
+
t1t3t4
+
t2t3t4
) |
|
Y = - c(t1t2t3t4)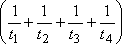
= c |
|
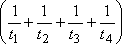 t1t2t3t4
= -1 |
|