| A system of circles having the same radical
axis are said to form a coaxal system. |
 |
| Condsider the equation of the radical
axis |
|
2(g - g')x
+ 2(f - f')y + C - C'
= 0
|
| (a) Let the centre of the circles lie
on the x-axis. |
| (b) Let the radical axis be the y-axis |
 |
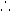f = f' = 0
, |
x = 0, |
C - C'
= 0 |
|
|
then
|
C = C' |
| Hence, the circles with the centre at
the x-axis is of the form |
x2 + y2
+ 2 x
+ C = 0
|
where C
is a constant and is
a parameter,
|
| have the y-axis as the radical axis |
| each value of determines
a circle of the coaxal system. |
| The circles x2
+ y2 + 2x
+ C = 0 |
| cut the radical axis x
= 0 at points where y2
+ C = 0 |
| (a) |
if C
< 0,
there are two real points of intersection
(0,  )
and
(0, -) |
|
| (b) |
if C
= 0, y
= 0
each circle touches the axis at (0,0) |
|
| (c) |
if C
> 0,
no point of intersection. |
|
| Consider the radius of the circles |
2
- C = r2
r = 
|
| Where r
= 0, |
the circle is a point circle 2
= C, =   |
| if C
< 0, |
no point circle |
| if C
= 0,
= 0 |
point circle is at the origin |
| if C
< 0,
= |
two point circles at (,0)
, (,0) |
|
| Circle : x2
+ y2 + 2x
+ C = 0 Limiting
points : (,
0) |
| The circle x2
+ y2 + 2g'x + 2f'y + C'
= 0 |
| passes through the limiting point (,
0) |
| if C2g'+
C'
=
0 |
| if C
+
C'
=
0 and
g'
= 0 |
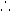circles of the form x2
+ y2 + 2 x
+ C = 0 ---(*) |
| passes through
the limiting point of the coaxal system given by |
x2 + y2
+ 2x
+ C = 0
| (a) |
(*) gives another coaxal system
of circles having centre on the radical axis of the first system and the
radical axis being the x-axis. |
| (b) |
If 2gg'
+ 2ff' - (C + C') = 0 |
|
Hence, any 2 circles search from either
system are orthogonal. |
|
|
